Друга вежба

Основне алгоритамске структуре и типови података

Нерешени задаци

Неке белешке...

Задатак 1.

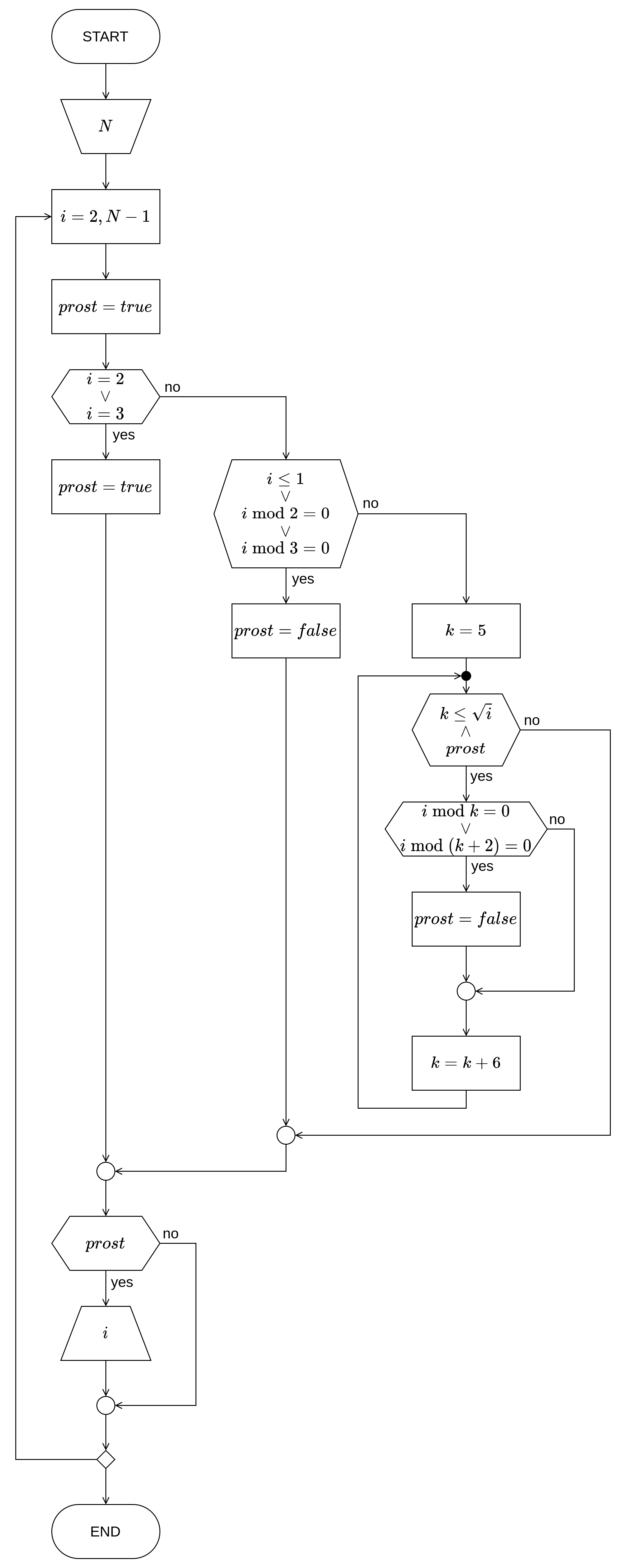
Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм који одређује и приказује све просте бројеве мање од \(N\). Целобројни параметар \(N\) уноси корисник. Уколико се при извршавању програма за \(N\) унесе вредност \(100\), шта ће програм приказати на излазу?

Териотисање

Хајде прво да направимо програм који одређује да ли је неки цео број (\(M \in \Z\)) прост.

Из математике знамо да се прост број дефинише као број који је дељив самим собом и бројем \(1\). Прецизније, прост број је онај који има тачно два, међусобно различита фактора (делиоца).

Број \(1\) се не сматра ни простим ни сложеним бројем, неки би рекли да јесте, а неки да није прост број. Управо како \(1\) има само један фактор, дељив је једино самим собом, не задовољава дефиницију просих бројева.

Применом овог знања долазимо до првог, „наивног” решења.

Нека унесемо цео број \(M\) и претпоставимо да јесте прост број. Употребићемо неки флег (енг. flag, променљива у којој чувамо неко стање програма) prost која ће у почетном тренутку имати вредност 1, што представља тачну вредност у програмском језику C када се употребљава као услов у наредби гранања (док све остале вредности представљају нетачну вредност, али се често за ту сврху користи 0 као нетачна вредност).

Поставићемо потом бројачку петљу, крећући се од првог простог броја \(2\), до претходника броја \(M\) (што ће бити \(M-1\)) и проверавати притом да ли је \(M\) дељиво са бројачем петље (нека је у овом случају \(P\) бројач петље). Проверу дељивости би вршили употребом модуло (остатка при дељењу) оператора (% у C-у).

Ако је остатак при дељењу једнак нули, одредили смо да број \(M\) није прост, те постављамо променљиву prost на 0.

Након петље, уколико нисмо оповргнули претпоставку (променљива prost је задржала почетну вредност \(1\)), штампамо тај број \(M\) на стандардни излаз. Како нисмо додали алтернативно гранање (else) уколико услов није задовољен (prost је променио вредност на \(0\)), програм неће исписати било какву поруку.

#include <stdio.h>

main() {
    int m, p, prost;

    m = 7; // Мењајте вредност променљиве за тестирање

    // Претпоставка да је број прост
    prost = 1;

    for (p = 2; p <= m - 1; p++) {
        if (m % p == 0) {
            // Оповргавамо претпоставку ако је
            // дељив бројем P
            prost = 0;
        }
    }

    if (prost) {
        printf("%d\n", m);
    }
}

Да би добили целокупно решење задатка, претходно одрађено је потребно сместити унутар још једне бројачке петље са бројачем \(M\), која ће се кретати бројевима од \(2\) до \(N - 1\) (јер се траже прости бројеви мањи од \(N\)) и затражити од корисника унос броја \(N\) на почетку програма.

Овим смо добили прво, наивно решење задатка.

#include <stdio.h>

main() {
    int n, m, p, prost;

    // Унос променљиве n као цео број
    scanf("%d", &n);

    for (m = 2; m <= n - 1; m++) {
        prost = 1;

        for (p = 2; p <= m - 1; p++) {
            if (m % p == 0) {
                prost = 0;
            }
        }

        if (prost) {
            printf("%d\n", m);
        }
    }
}

Сувишно је вршити проверу дељења броја \(M\) са бројевима редом од \(2\) до \(M - 1\). Сви делиоци броја \(M\) (без њега самог) биће мањи од или једнаки \(\frac{M}{2}\). Нпр. \(1, 2, 4, 5, 10, 20, 25, 50\) су делиоци броја \(100\), а највећи је \(50\). Додатно, можемо уочити понављање производа у факторизацији броја \(100\), \(2 \cdot 50, 4 \cdot 25, 5 \cdot 20, 10 \cdot 10, 20 \cdot 5, 50 \cdot 2\) – парови \(2 \cdot 50\) и \(50 \cdot 2\), \(4 \cdot 25\) и \(25 \cdot 4\), \(5 \cdot 25\) и \(25 \cdot 5\), су сачињени од истих бројева. Ово важи за било који број, тако да није потребно трагати даље од \(\sqrt{M}\) (што ће за дат пример броја \(100\) бити \(10\), факторизација у средини сачињена од два иста броја).

Уколико оповргнемо претпоставку да број није прост, и даље ће програм наставити да проверава дељивост са наредним бројем у следећој итерацији петље, иако је то управо скроз сувишно. Да бисмо то заобишли, свешћемо унутрашњу бројачку петљу у еквивалентну while петљу, потом употребом конјункције (\(\land\) - логичко И, && оператор у C-у) услову петље придодати услов „све док је \(M\) број прост” (све док променљива prost има тачну вредност \(1\)).

Резултујућа унутрашња петља применом ове две оптимизације постаје:

        p = 2;
        while (prost && p <= sqrt(m)) {
            if (m % p == 0) {
                prost = 0;
            }
            p++;
        }

У програму је још потребно додати линију #include <math.h> изнад главног програма (main()) како би било могуће употребити математичку функцију за одређивање квадратног корена броја sqrt(x) (square root) дефинисану управо у заглављу math.h.

Овакво добијено решење је сасвим довољно оптимално, али наравно може се још оптимизовати даљом употребом математичког размишљања:

Даћемо пример привх 10 простих бројева: \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29\).
Приметимо да је први прост број \(2\), други је \(3\), и тако даље. Осим броја \(2\) који је и једини паран прост број, сви остали прости бројеви су заправо непарни (јер је сваки паран број дељив и бројем \(2\), па онда такви бројеви, сем броја \(2\), нису прости).

Претходно је речено да је први прост број \(2\), а други \(3\). Дакле уколико је \(M = 3 \lor M = 2\), знамо да број \(M\) јесте прост.

Ако је број дељив са \(2\) или \(3\) (\(M \bmod 2 = 0 \lor M \bmod 3 = 0\)), број није прост.

Негативни бројеви нису прости бројеви, јер су сви дељиви барем са \(-1\). \(0\), слично броју \(1\), није ни прост ни сложен број – број \(0\) подељен самим собом није дефинисано и сваки други број је могуће поделити са \(0\). Бројеви мањи или једнаки \(1\) (\(N \leq 1\)) нису прости бројеви, мада у овом задатку петљом смо ограничили да проверу почињемо од првог познатог простог броја \(2\), те је сувишно уврстити овај услов у програм.

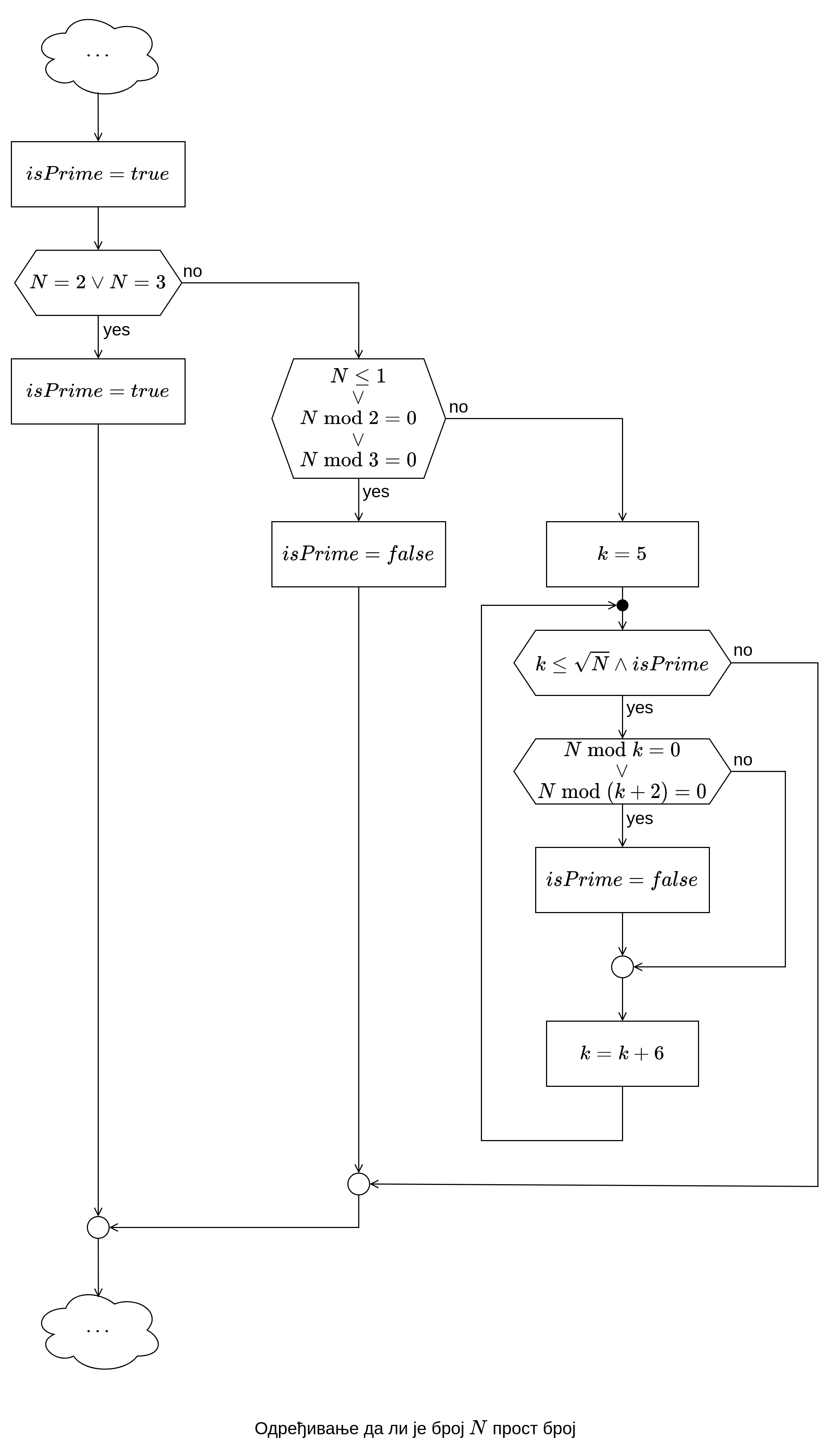
Дакле, на основу свега изнад речено, уколико је \(M\) различито од \(2\) и \(3\) и ако га је могуће поделити са \(2\) или \(3\), такав број није прост. Уколико је услов \(M \neq 2 \land M \neq 3 \land (M \bmod 2 = 0 \lor M \bmod 3 = 0)\) испуњен, број није прост. У супротном настављамо са даљом провером:

Све целе бројеве је могуће представити у облику \(6k+i\), за \(k \in \Z\) и \(i = -1, 0, 1, 2, 3, 4\). Број \(2\) дели бројеве облика \(6k\), \(6k+2\) и \(6k+4\), а број \(3\) дели бројеве облика \(6k+3\), што смо условом изнад већ покрили. Када је \(k \leq 0\) тада је број нула или негативан, што уопште и не разматрамо у програму, већ бројеве који се крећу од \(2\) до крајњег \(N - 1\). Остаје једино проверити да ли је \(M\) дељив са свим бројевима мањи од или једнаке \(\sqrt{M}\) који су облика \(6k \pm 1\) за \(k \geq 1\).

У почетном тренутку можемо да поставимо \(P = 5\), тј. за почетни тренутак када је \(k = 1 \Rightarrow 6k - 1 = 5\). Уколико је \(М\) дељиво са \(P\) (\(6k - 1\)) или \(P + 2\) (\(6k + 1\)) онда оповргавамо претпоставку да је \(M\) прост број. Петља се извршава све док важи услов \(prost \land P \leq \sqrt{M}\), при том на крају сваке итерације петље се \(P\) повећава за \(6\) и на тај начин заобилазимо потребу додавања променљиве \(k\) и операције множења броја. Додатно можемо заобићи употребу функције sqrt(x) у програмском коду тако што би услов \(P \leq \sqrt{M}\) заменили еквивалентним \(P^2 \leq M\). Све ово даље доноси већу ефикасности у употреби процесора и меморије програма.

Уколико је \(prost = 1\), штампамо број \(M\).

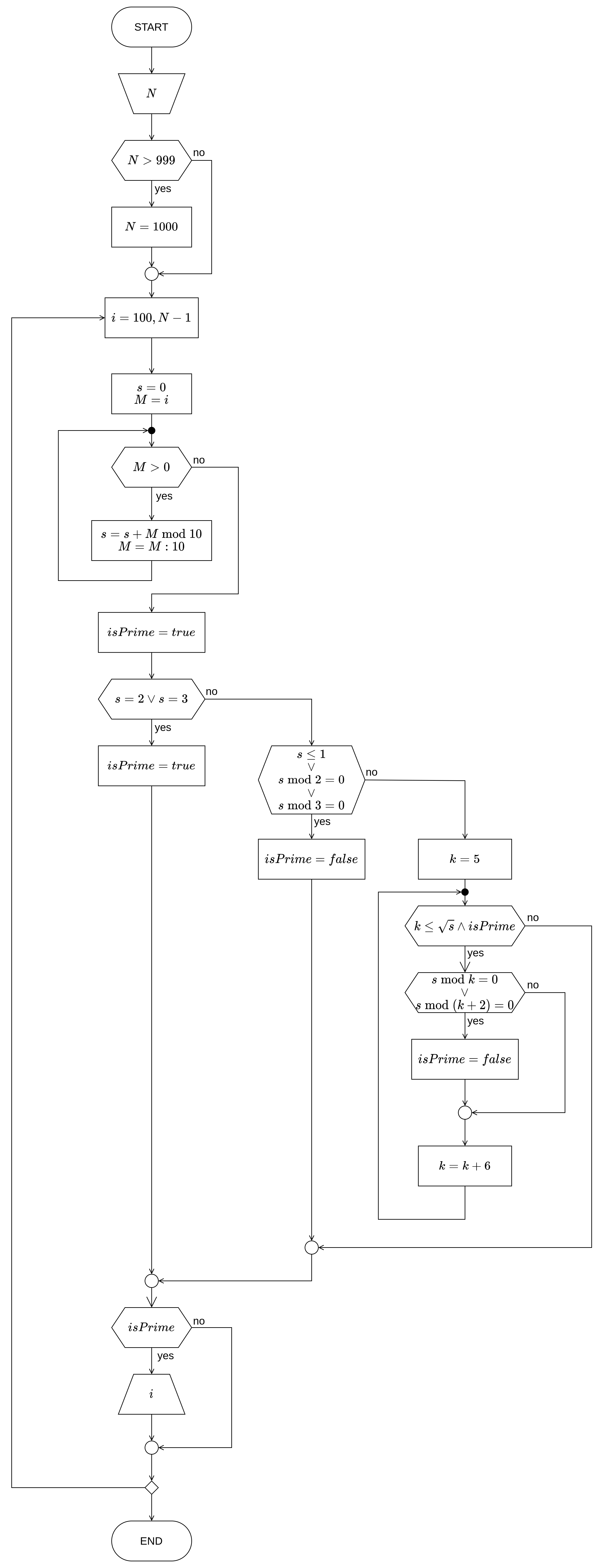
Дијаграм тока алгоритма

Наивно решењеОптимално решењеОптимизовано решење

Изворни код програма

Наивно решењеОптимално решењеОптимизовано решење

#include <stdio.h>

main() {
    int n, m, p, prost;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (m = 2; m <= n - 1; m++) {
        prost = 1;

        for (p = 2; p <= m - 1; p++) {
            if (m % p == 0) {
                prost = 0;
            }
        }

        if (prost) {
            printf("%d\n", m);
        }
    }
}

#include <stdio.h>
#include <math.h>

main() {
    int n, m, p, prost;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (m = 2; m <= n - 1; m++) {
        prost = 1;

        p = 2;
        while (prost && p <= sqrt(m)) {
            if (m % p == 0) {
                prost = 0;
            }
            p++;
        }

        if (prost) {
            printf("%d\n", m);
        }
    }
}

#include <stdio.h>

main() {
    int n, m, p, prost;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (m = 2; m < n; m++) {
        prost = 1;

        if (m > 3 && (m % 2 == 0 || m % 3 == 0))
            prost = 0;
        else {
            p = 5;
            while (prost && p * p <= m) {
                if (m % p == 0 || m % (p + 2) == 0) {
                    prost = 0;
                }

                p += 6;
            }
        }

        if (prost) {
            printf("%d\n", m);
        }
    }
}

Алтернативно решење

Упозорење!

Ово решење користи елементе програмирања који нису предвиђени за извођење ове вежбе. У овом решењу су коришћени низови (поља) који су предвиђени за извођење наредне, треће, лабораторијске вежбе и овде неће бити објашњени!

За решавање овог задатка погодно је искористити алгоритам „Ератостеново сито”:

1. Направити низ целих бројева од \(2\) до \(N\), \(\{2, 3, 4, …, N\}\);
2. Нека је \(p = 2\), најмањи прост број;
3. У низу означити бројеве који су умношци \(p\)–а (\(2p, 3p, 4p, …\));
4. Пронаћи најмањи број у низу већи од \(p\) који није означен. Тај број поставити као нову вредност \(p\)–а, поновити претходни корак. Уколико такав број не постоји, крај алгоритма;
5. Преостали, неозначени бројеви по завршетку алгоритма биће само прости бројеви мањи од \(N\).

Пример, корак по корак

Легенда:
x – неозначен елемент, разматра се као прост број;
x – неозначен елемент у односу на који се његови умношци означавају;
x – означен елемент у тренутном кораку алгоритма, одредили смо да није прост број;
x – означен елемент у претходним корацима, није прост број;
x – означен елемент у тренутном кораку који је већ био претходно означен.

Генерисати низ од \(N = 100\) елемената, од \(1\) до \(N\). Притом, први елемент \(1\) не разматрамо и занемарујемо. Ради прегледности, низ је представљен у 10 редова.

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

У почетку разматрамо \(2\), најмањи прост број. Означавамо све елементе низа који су умношци броја \(2\). Дакле, означени бројеви биће \(\{ 4, 6, 8, …, 100 \}\).

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

Наредни неозначени број након броја \(2\) је број \(3\). Означавамо све елементе низа који су умношци броја \(3\). Означени бројеви биће \(\{ 6, 9, 12, …, 99 \}\).

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

Поступак понављамо за број \(5\).

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

Поступак понављамо за број \(7\).

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

Поступак понављамо за број \(11\). Овде можемо приметити да сви означени бројеви у овом кораку су већ претходно били означени, стога се овде алгоритам завршава. Из овога можемо закључити да се алгоритам завршава у тренутку када \(p\) постане веће од \(\sqrt{N}\). \(11 > \sqrt{100}\), тј. \(11 > 10\). Односно, алгоритам се извршава све док је \(p \le \sqrt{N}\), тј. \(p^2 \le N\).

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

На крају, низ изгледа овако:

/ 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100

Односно, прости бројеви мањи од \(N = 100\) одређени Ератостеновим ситом су \(\{ 2, 3, 5,\) \(7, 11, 13, 17,\) \(19, 23, 29,\) \(31, 37, 41,\) \(43, 47, 53,\) \(59, 61, 67,\) \(71, 73, 79, 83,\) \(89, 97 \}\).

Додатне белешке

Претходно је објашњена класична реализација алгоритма „Ератостеново сито”. Поновним посматрањем датог примера изнад, корак по корак, можемо осматрати однос између тренутно посматраног елемента за који знамо да је наредни прост број (p) и првог означеног елемента који није био означен у претходним корацима (x). Приметимо да је \(x = p^2\), тако да означавање елемената можемо почети од \(p^2\), уместо од \(2p\) и самим тим уштедимо на времену.

Алгоритам

Изворни код

#include <stdio.h>

main() {
    int n, i, p;
    int primes[100];

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (i = 0; i < n; i++) {
        primes[i] = 1;
    }

    for (p = 2; p * p < n; p++) {
        if (primes[p]) {
            for (i = p * p; i < n; i += p) {
                primes[i] = 0;
            }
        }
    }

    for (p = 2; p < n; p++) {
        if (primes[p]) {
            printf("%d\n", p);
        }
    }
}

///

Задатак 2.

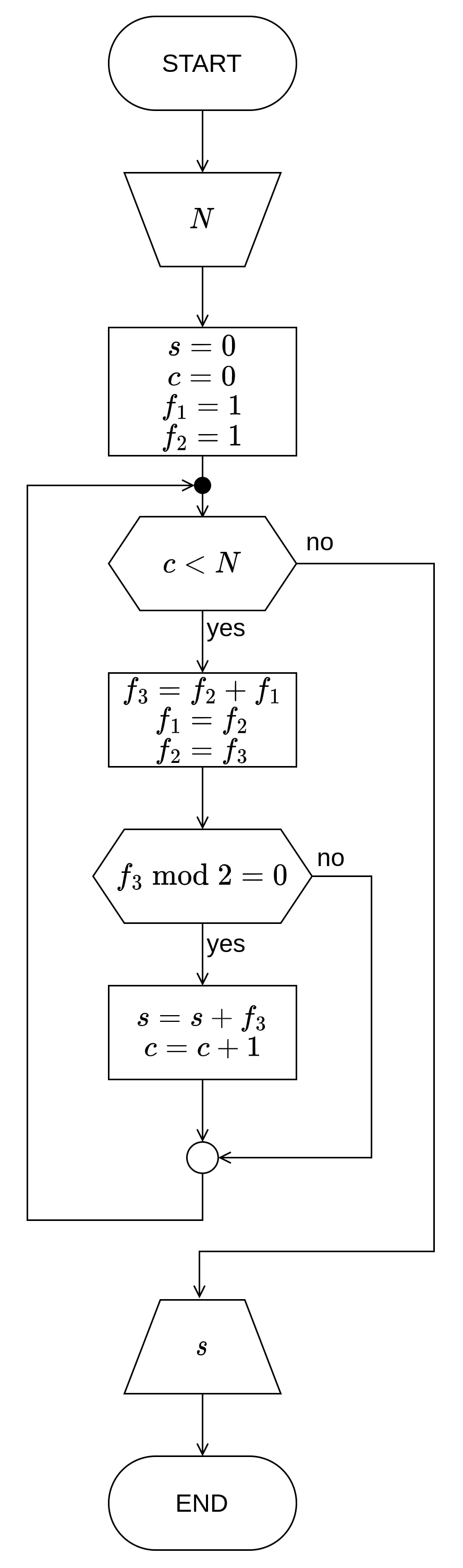
Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм који одређује и приказује суму првих \(N\) парних чланова Фибоначијевог низа. Параметар \(N\) задаје корисник, подразумевати да је \(N \geq 3\). Елементи фибоначијевог низа су дати формулом \(f_i = f_{i-1} + f_{i-2}\) за \(i \geq 3\), где је \(f_1 = f_2 = 1\). Уколико се при извршавању програма за \(N\) унесе вредност \(10\), шта ће програм приказати на излазу?

Териотисање

Чланови Фибоначијевог низа су дати рекурзивном формулом. Како би било могуће израчунати неки члан Фибоначијевог низа, потребно је познавати вредности њему два претходна члана, чија вредност такође зависи од њима претходним члановима, и тако даље… Познато је (дато задатком) да први (\(f_1\)) и други (\(f_2\)) члан Фибоначијевог низа има вредност \(1\). За израчунавање трећег члана, применом формуле, добијамо \(f_3 = f_2 + f_1 = 1 + 1 = 2\). Сада када знамо и трећи члан, можемо наћи и четврти: \(f_4 = f_3 + f_2 = 2 + 1 = 3\)… Овај поступак се може понављати док се не дође до траженог \(N\)–тог, \(f_N\), члана.

Како редом одређујемо чланове Фибоначијевог низа у петљи, у тренутку када је тренутно нађени члан паран број (\(f_i \bmod 2 = 0\)), додати га суми и инкрементовати вредност неког бројача (\(c = c + 1\)). Овај процес се понавља све док је \(c < N\).

"Може и бројачка петља!"

Уколико би исписали првих, рецимо 9, чланова Фибоначијевог низа – 1, 1, 2, 3, 5, 8, 13, 21, 34 – можемо приметити да су први и други непарни бројеви, трећи је паран, четврти и пети непарни, шести паран, седми и осми непарни и девети паран. То ће наравно увек важити, јер сабирањем непарног и парног броја добијамо непаран број, док сабирањем два непарна добијамо паран број. Дакле, сваки трећи члан је паран па можемо и срачунати колики број проласка нам је потребан како би дошли до \(N\) парних чланова, односно то би било \(3N\) проласка петље.

Дијаграм тока алгоритма

Изворни код програма

whilefor

#include <stdio.h>

main() {
    int n, c = 0;
    long f1 = 1, f2 = 1, f3, s = 0;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    while (c < n) {
        f3 = f2 + f1;
        f1 = f2;
        f2 = f3;

        if (f3 % 2 == 0) {
            s += f3;
            c++;
        }
    }

    printf("Suma %d parnih clanova Fibonacijevog niza iznosi %lld.\n", c, s);
}

#include <stdio.h>

main() {
    int n, i;
    long f1 = 1, f2 = 1, f3, s = 0;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (i = 0; i < 3 * n; i++) {
        f3 = f2 + f1;
        f1 = f2;
        f2 = f3;

        if (f3 % 2 == 0) {
            s += f3;
        }
    }


    printf("Suma %d parnih clanova Fibonacijevog niza iznosi %lld.\n", i / 3, s);
}

Задатак 3.

Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм којим се одређују и приказују сви троцифрени бројеви мањи од \(N\) чији је збир цифара прост број. Целобројни параметар \(N\) задаје корисник. Уколико се при извршавању програма за \(N\) унесе вредност \(120\), шта ће програм приказати на излазу?

Териотисање

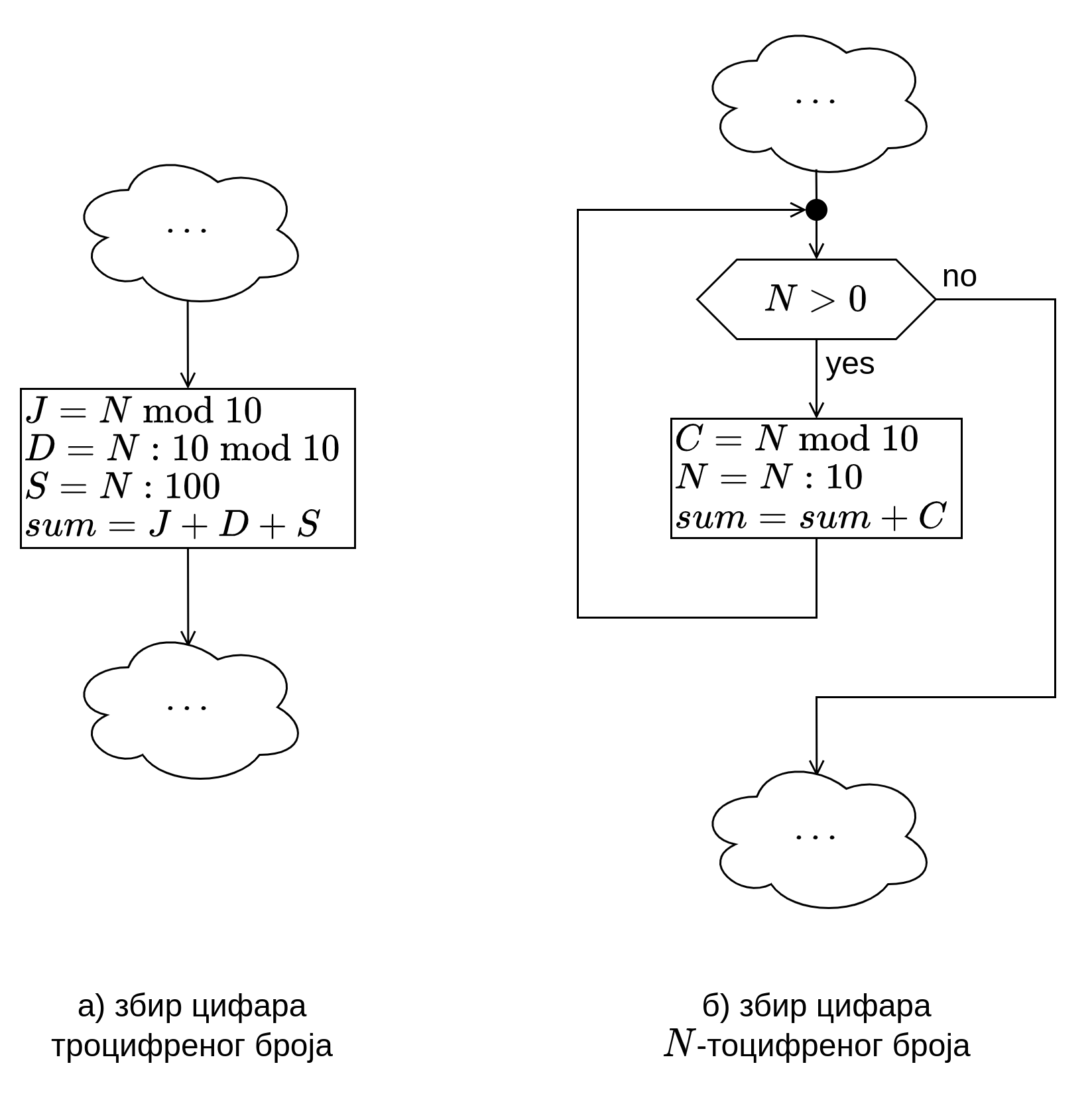
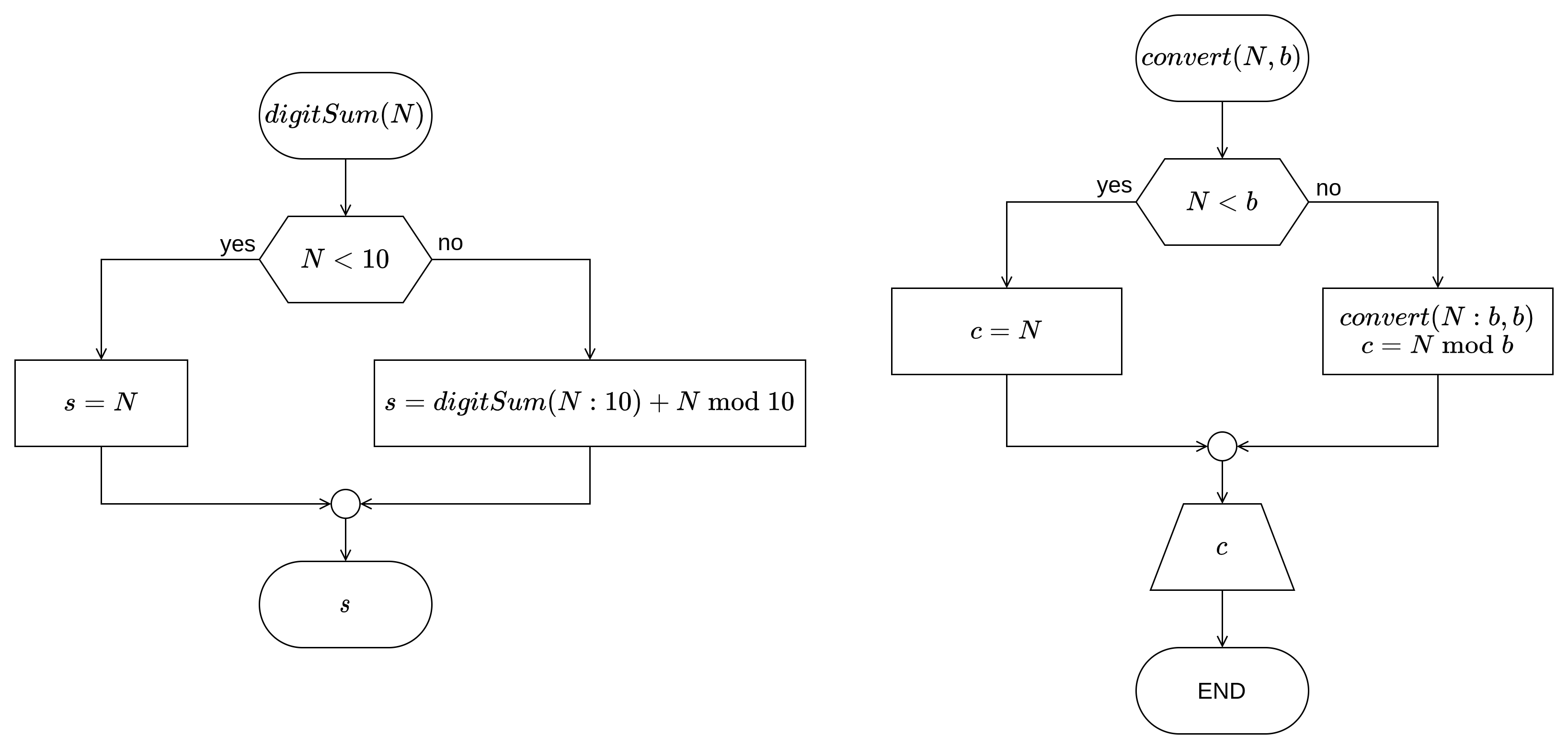
Како би одредили збир цифара троцифреног броја, потребно је на неки начин раставити цифре из броја. Познато нам је да је троцифрен број симболички записан као \(SDJ\) могуће записати као \(S \cdot 100 + D \cdot 10 + J \cdot 1\), где је \(S\) стоти део, \(D\) десети део, \(J\) јединица броја. Нпр. \(834 = 8 \cdot 100 + 3 \cdot 10 + 4 \cdot 1\). Дељењем таквог броја са \(10\) добијамо број облика \(SD\), тј. одстранили смо \(Ј\), што је уједно и остатак при дељењу. Применом оператора дељења (\(:\), тј. \(/\)) и остатка при дељењу (\(\bmod\), тј. \(\%\)) можемо одвојити цифре броја.

\[ \begin{aligned} SDJ \bmod 10 = J \\ SDJ : 10 \bmod 10 = D \\ SDJ : 100 = S \\ \end{aligned} \]

Слично, могуће је исто применити за било који број, ма колико цифара он поседовао. Претходно дат пример се може записати и у облику \(S \cdot 10^2 + D \cdot 10^1 + J \cdot 10^0\). Можемо приметити да се цифра множи са бројем \(10\) (основом бројног система/различит број могућих цифара) на степену који одговара тежини цифре, почевши од тежине једнаке \(0\) за цифру јединице. С обзиром на то, добијен алгоритам можемо генералисати за било који \(N\)–тоцифрени број – кроз сваки пролазак петље одредити цифру најмање тежине броја \(N\) као \(N \bmod 10\), потом поделити \(N\) са \(10\) и сачувати резултат у \(N\) и понављати све док је \(N \gt 0\).

Важно је напоменути да се овим поступком мења вредност броја \(N\); Уколико би желели да сачувамо почетну вредност (коју је корисник унео), потребно је пре бројачке петље сачувати \(N\) у неку помоћну променљиву и потом користити \(N\) у петљи, а помоћну изван петље где нам треба уместо \(N\) или обрнуто.

Када смо одвојили цифре, потребно их је сабрати и корак смо ближи решењу задатка.

Напослетку, потребно је одредити да ли је сума цифара прост број.

Из 1. задатка знамо како да одредимо да ли је број прост. Када знамо да су први прости бројеви бројеви \(2\) и \(3\), онда било шта са фактором \(2\) или \(3\) није прост број. Уколико претходни услови нису задовољени проверавамо даље петљом од наредног познатог простог броја \(5\) до корена траженог броја, \(\sqrt{N}\), са кораком од \(6\); Ако је остатак при дељењу броја \(N\) са \(k\) или \(k+2\) једнак \(0\), где је \(k\) бројач петље, број \(N\) није прост број. У супротном, ако је остатак при дељењу \(N\) са свако \(k\) и \(k+2\) различито од \(0\), онда је број \(N\) прост. Негативни бројеви нису прости (јер је сваки могуће поделити барем са \(-1\)), као и бројеви \(0\) и \(1\) (ни прости ни сложени).

Уколико је \(N > 999\) кореговати га на \(N = 1000\). Бројачком петљом од \(100\) до \(N - 1\) пролазимо кроз све троцифрене бројеве, мање од \(N\). Склапањем горе наведених елемената решења у петљи добијамо и крајњи програм за решавање овог задатка.

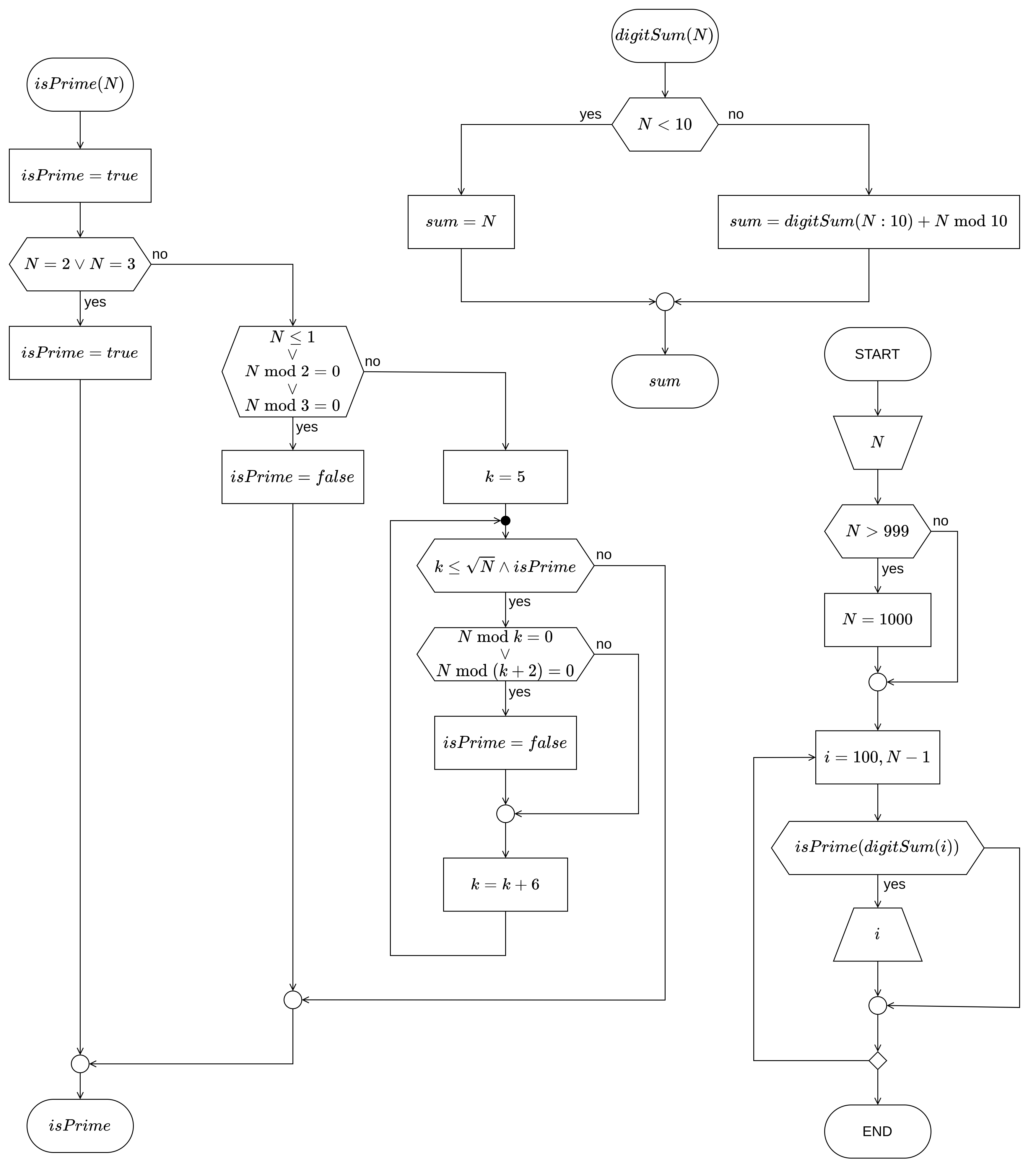
Дијаграм тока алгоритма

Изворни код програма

#include <stdio.h>

main() {
    int n, i, k, s, m, isPrime;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    if (n > 999)
        n = 1000;

    for (i = 100; i < n; i++) {
        s = 0;
        m = i;

        while (m > 0) {
            s += m % 10;
            m /= 10;
        }

        isPrime = 1;

        if (s == 2 || s == 3) {
            isPrime = 1;
        }

        else if (s <= 1 || s % 2 == 0 || s % 3 == 0) {
            isPrime = 0;
        }

        else {
            k = 5;
            while (k * k <= s && isPrime) {
                if (s % k == 0 || s % (k + 2) == 0) {
                    isPrime = 0;
                }

                k += 6;
            }
        }

        if (isPrime) {
            printf("%d\n", i);
        }
    }
}

Алтернативно решење

Упозорење!

Ово решење користи елементе програмирања који нису предвиђени за извођење ове вежбе. У овом решењу су коришћене функције (са рекурзивним позивом) које су предвиђене за извођење пете лабораторијске вежбе и овде неће бити објашњене!

Коришћење функција је погодно како би се одвојили логички делови ко̑да и омогућило лакше коришћење истог ко̑да без његовог дупликовања. Самим тим, код у главом програму (main() функцији) биће минималнији и прегледнији и лакше је одредити функционалност ко̑да прегледом назива позваних функција.

Алгоритам

Изворни код

#include <stdio.h>

int digitSum(int n)
{
    return n < 10 ? n : digitSum(n / 10) + n % 10;
}

int isPrime(int n)
{
    int k, isPrime = 1;

    if (n == 2 || n == 3) isPrime = 1;
    else if (n <= 1 || n % 2 == 0 || n % 3 == 0) isPrime = 0;
    else {
        k = 5;
        while (k * k <= n && isPrime) {
            if (n % k == 0 || n % (k + 2) == 0)
                isPrime = 0;
            k += 6;
        }
    }

    return isPrime;
}

main() {
    int n, i;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    if (n > 999)
        n = 1000;

    for (i = 100; i < n; i++) {
        if (isPrime(digitSum(i))) {
            printf("%d\n", i);
        }
    }
}

Задатак 4.

Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм којим се одређују и приказују сви троцифрени бројеви чији је збир цифара једнак 17, а притом су дељиви са \(K\). Целобројни параметар \(K\) задаје корисник. Уколико се при извршавању програма за \(K\) унесе вредност \(7\), шта ће програм приказати на излазу?

Териотисање

У претходном, 3. задатку, приказано је већ одређивање збир цифара троцифреног, као и \(N\)–тоцифреног броја. Одређивање дељивости два броја могуће је провером да ли је остатак при дељењу два броја једнак \(0\), што добијамо употребом \(\bmod\)–уло оператора (\(\%\) у C програмском језику). Пуштањем бројачке петље од \(100\) до \(999\) са провером да ли је збир цифара броја једнак \(17\) и да ли је тренутно посматран троцифрен број дељив са унетим бројем \(К\), и ако јесте исписом тог броја, је управо и решење овог задатка.

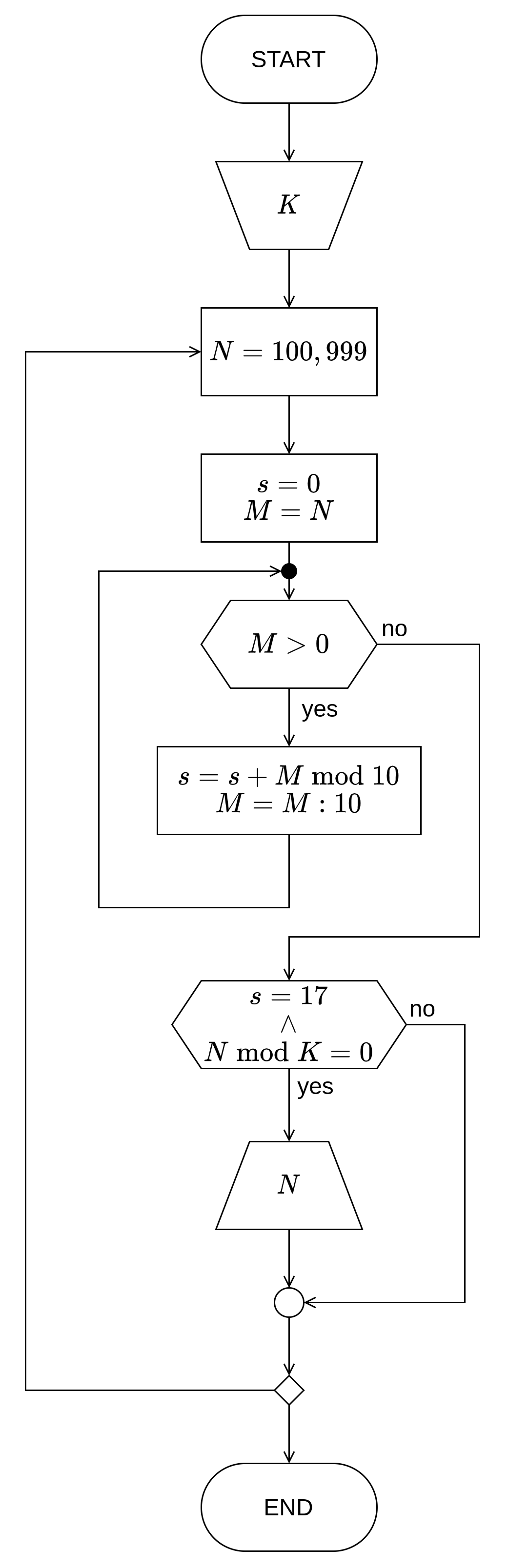
Дијаграм тока алгоритма

Изворни код програма

#include <stdio.h>

main() {
    int k, n, s, m;

    printf("Unesite ceo broj K: ");
    scanf("%d", &k);

    for (n = 100; n < 1000; n++) {
        s = 0;
        m = n;

        while (m > 0) {
            s += m % 10;
            m /= 10;
        }

        if (s == 17 && n % k == 0) {
            printf("%d\n", n);
        }
    }
}

Задатак 5.

Нацртати структурни дијаграм тока алфоритма и на програмском језику C написати структурни програм који одређује збир цифара задатог целог броја \(B\). Број цифара броја није унапред познат. Показати модификације претходног решења помоћу којих се може одредити:
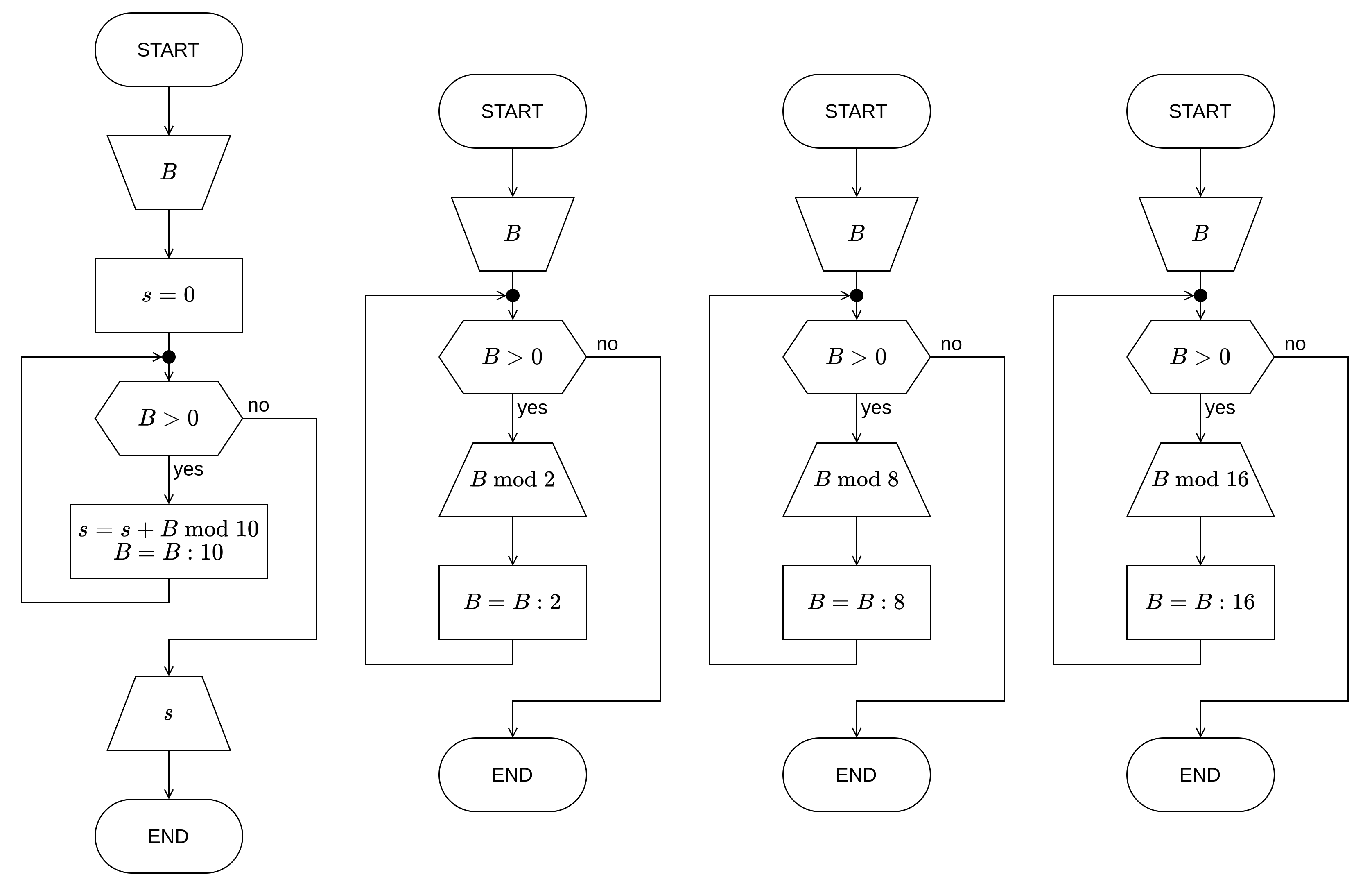
а) бинарна репрезентација задатог броја,
б) октална репрезентација задатог броја,
в) хексадекадна репрезентација задатог броја.

Напомена

Цифре у решењима под а, б и в приказивати редоследом којим су добијене.

Уколико се при извршавању програма за \(B\) унесе вредност \(138\), шта ће програм приказати на излазу?

Териотисање

Збир цифара \(N\)–тоцифреног броја је већ обрађено у 3. задатку – идеја је једноставна, када поделимо неки број са \(10\) остатак при дељењу је цифра јединица (цифра најмање тежине, која се налази скроз десно), а количник је број са једном цифром мање. Понављањем поступка можемо редом одвајати цифре и сумирати их.

Модификација решења за проналажење бинарне, окталне или хексадекадне репрезентације броја је проста – уместо одвајања цифара са \(10\) (базом декадног бројног система), чинићемо то са \(2\), \(8\), односно \(16\), и потом уместо сумирање цифара, приказивати их. Цифре добијене на овакав начин биће у супротном редоследу него што би требале да буду превођењем броја у тражене бројне системе, што сам задатак и налаже да тако и треба бити из напомене.

Дијаграм тока алгоритма

Изворни код програма

"Форматиран улаз/излаз"

Испод су дата два слична решења. Једно решење користи само %d и %c при штампању, док друго користи %d, %o и %x.

• %d исписује цео број као декадни (d = decimal);
• %o исписује цео број као октални (o = octal);
• %x исписује цео број као хексадекадни (x = hex);
• %c исписује цео број као ASCII карактер по кодној вредности (c = character).

Да ли користили %o или %d у овом решењу за штампање окталних цифара, разлике нема.

Формат за приказивање броја у бинарном формату не постоји, па ту можемо употребити који год формат за целе бројеве сем %c.

Једина разлика је при штампању цифре хексадекадног броја – са %x рачунар ће аутоматски протумачити и превести декадни број \(10\) у A, \(11\) у B, \(12\) у C, … Уколико користимо %d, не би се у сваком случају штампала нужно хексадекадна цифра па је онда потребно додати проверу уколико је број већи или једнак \(10\), употребити %c формат и штампати путем њега вредност 'A' + cifra - 10, односно 'а' + cifra - 10. Ово функционише, јер као што је то случај и у енглеском алфабету, слова су редом поређана у ASCII табели, а с обзиром на то да је знаковни тип (char) у C програмском језику бројевни тип, аритметика са карактерима и бројевима је дозвољена и резултат ће бити нова бројчана вредност, односно један карактер (зависно од тумачења, тј. коришћеног форматирања при испису).

Са %d и %cСа %d, %o и %x

#include <stdio.h>

main() {
    int b, n, s = 0;

    printf("Unesite ceo broj B: ");
    scanf("%d", &b);

    n = b;
    while (n > 0) {
        s += n % 10;
        n /= 10;
    }

    printf("Zbir cifara: %d\n", s);

    printf("\na) binarna reprezentacija: ");
    n = b;
    while (n > 0) {
        printf("%d", n % 2);
        n /= 2;
    }

    printf("\nb) oktalna reprezentacija: ");
    n = b;
    while (n > 0) {
        printf("%d", n % 8);
        n /= 8;
    }

    printf("\nc) heksadekadna reprezentacija: ");
    n = b;
    while (n > 0) {
        int c = n % 16;
        if (c < 10) {
            printf("%d", c);
        } else {
            printf("%c", 'A' + c - 10);
        }
        n /= 16;
    }
}

#include <stdio.h>

main() {
    int b, n, s = 0;

    printf("Unesite ceo broj B: ");
    scanf("%d", &b);

    n = b;
    while (n > 0) {
        s += n % 10;
        n /= 10;
    }

    printf("Zbir cifara: %d\n", s);

    printf("\na) binarna reprezentacija: ");
    n = b;
    while (n > 0) {
        printf("%d", n % 2);
        n /= 2;
    }

    printf("\nb) oktalna reprezentacija: ");
    n = b;
    while (n > 0) {
        printf("%o", n % 8);
        n /= 8;
    }

    printf("\nc) heksadekadna reprezentacija: ");
    n = b;
    while (n > 0) {
        printf("%x", n % 16);
        n /= 16;
    }
}

Алтернативно решење

Упозорење!

Ово решење користи елементе програмирања који нису предвиђени за извођење ове вежбе. У овом решењу су коришћене функције (са рекурзивним позивом) које су предвиђене за извођење пете лабораторијске вежбе и овде неће бити објашњене!

Коришћење рекурзивне функције је погодно у овом случају како би лако имплементовали алгоритам суме цифара и потом га модификовати да приказује репрезентацију броја у било ком позиционом бројном систему уз тачан редослед приказивања цифара.

Додатно је приказана и још једна модификација у којој се употребљавају ниске (string–ови), низови карактера, што је предвиђено тек за задњу, шесту, лабораторијску вежбу.

Алгоритам

Изворни код

Штампање из функцијеШтампање из главног програма (са нискама)

#include <stdio.h>

int digitSum(int n) {
    int sum;

    if (n < 10) {
        sum = n;
    } else {
        sum = digitSum(n / 10) + n % 10;
    }

    return sum;
}

void convert(int n, int b) {
    int c;

    if (n < b) {
        c = n;
    } else {
        convert(n / b, b);
        c = n % b;
    }

    if (c < 10) {
        printf("%d", c);
    } else {
        printf("%c", 'A' + c - 10);
    }
}

main() {
    int b;

    printf("Unesite ceo broj B: ");
    scanf("%d", &b);

    printf("Zbir cifara: %d\n", digitSum(b));

    printf("\na) binarna reprezentacija: ");
    convert(b, 2);

    printf("\nb) oktalna reprezentacija: ");
    convert(b, 8);


    printf("\nc) heksadekadna reprezentacija: ");
    convert(b, 16);
}

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

int digitSum(int n) {
    int sum;

    if (n < 10) {
        sum = n;
    } else {
        sum = digitSum(n / 10) + n % 10;
    }

    return sum;
}

char getChar(int c) {
    return c < 10 ? '0' + c : 'A' + c - 10;
}

char *appendChar(char *str, char c) {
    int i = 0;

    while (str[i] != '\0') {
        i++;
    }

    str[i] = c;
    str[i + 1] = '\0';

    return str;
}

char *convertStr(int n, int b) {
    char *str = malloc(32);
    char c;

    if (str == NULL) {
        printf("Failed to allocate memory!");
        exit(1);
    }

    if (n < b) {
        c = getChar(n);
    } else {
        c = getChar(n % b);
        strcat(str, convertStr(n / b, b));
    }

    appendChar(str, c);

    return str;
}

main() {
    int b;

    printf("Unesite ceo broj B: ");
    scanf("%d", &b);

    printf("Zbir cifara: %d\n\n", digitSum(b));

    printf("a) binarna reprezentacija: %s\n", convertStr(b, 2));
    printf("b) oktalna reprezentacija: %s\n", convertStr(b, 8));
    printf("c) heksadekadna reprezentacija: %s\n", convertStr(b, 16));
}

Задатак 6.

Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм који за првих \(N\) природних бројева одређује и приказује њихове факторијеле, као и факторијеле њихових квадрата. Параметар \(N\) задаје корисник. Уколико се при извршавању програма за \(N\) унесе вредност \(10\), шта ће програм приказати на излазу?

Дијаграм тока алгоритма

Изворни код програма

#include <stdio.h>

main() {
    int n, i, j;
    long double fact = 1, factSquare = 1;
    /* Sa `long double` moze se precizno racunati do 25!
     * Za vece faktorijele su pogresne vrednost, ali su na prvi pogled slicne u ciframa vecih tezina.
     * Pojasnjenje - https://stackoverflow.com/a/53387530 */

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (i = 1; i <= n; i++) {
        fact *= i;

        for (j = i * i; j > (i - 1) * (i - 1); j--) {
            factSquare *= j;
        }

        printf("%3d! = %26.0Lf, %3d! = %26.0Lf\n", i, fact, i * i, factSquare);
    }
}

Пример решења за рачунање факторијела било ког броја

Ово је чисто информативно решење које користи елементе наредних лабораторијских вежби, низове и функције, и решење ове комплексности није икада потребно репродуковати на овом курсу.

Како би превазишли ограниченост типова података програмског језика, сваку цифру можемо посебно чувати у меморији и максималан број цифара мењати у односу на то за колико велику прецизност нам је потребно да програм израчуна факторијел броја. С обзиром на то да су цифре, у низу, посебно сачуване, вршење аритметичких операција је мало компликованије јер бисмо морали суштински све операције да примењујемо корак по корак, цифра по цифру редом, као како би то чинили на папиру.

#include <stdio.h>

#define DIGITS 200

void clear(int a[DIGITS]) {
    int i;

    for (i = 0; i < DIGITS; i++) {
        a[i] = 0;
    }
}

void print(int a[DIGITS], int p) {
    int i;

    for (i = p - 1; i >= 0; i--) {
        printf("%d", a[i]);
        if (i % 3 == 0 && i > 2) {
            printf(" ");
        }
    }
    printf("\n");
}

int toDigits(int n, int a[DIGITS]) {
    int p = 0;

    clear(a);

    while (n > 0) {
        a[p++] = n % 10;
        n /= 10;
    }

    return p;
}

int countDigits(int a[DIGITS]) {
    int i = DIGITS - 1;

    while (i > 0 && a[i] == 0) {
        i--;
    }

    return i + 1;
}

int multiply(int a[DIGITS], int b[DIGITS], int p, int q, int prod[DIGITS]) {
    int i, j, carry;

    clear(prod);

    for (j = 0; j < q; j++) {
        carry = 0;
        for (i = 0; i < p; i++) {
            prod[i + j] += carry + a[i] * b[j];
            carry = prod[i + j] / 10;
            prod[i + j] %= 10;
        }

        prod[j + p] = carry;
    }

    return countDigits(prod);
}

int copy(int a[DIGITS], int p, int b[DIGITS]) {
    int i;

    for (i = 0; i < p; i++) {
        b[i] = a[i];
    }

    return p;
}

main() {
    int n, m, o, a[DIGITS], b[DIGITS], c[DIGITS], d[DIGITS], p, q, r, s;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    p = toDigits(1, a);
    q = toDigits(1, b);

    for (m = 1; m <= n; m++) {
        r = toDigits(m, c);
        s = multiply(a, c, p, r,d);
        p = copy(d, s, a);

        for (o = m * m; o > (m - 1) * (m - 1); o--) {
            r = toDigits(o, c);
            s = multiply(b, c, q, r, d);
            q = copy(d, s, b);
        }

        printf("%d! = ", m);
        print(a, p);
        printf("%d! = ", m * m);
        print(b, q);
        printf("\n");
    }
}

Задатак 7.

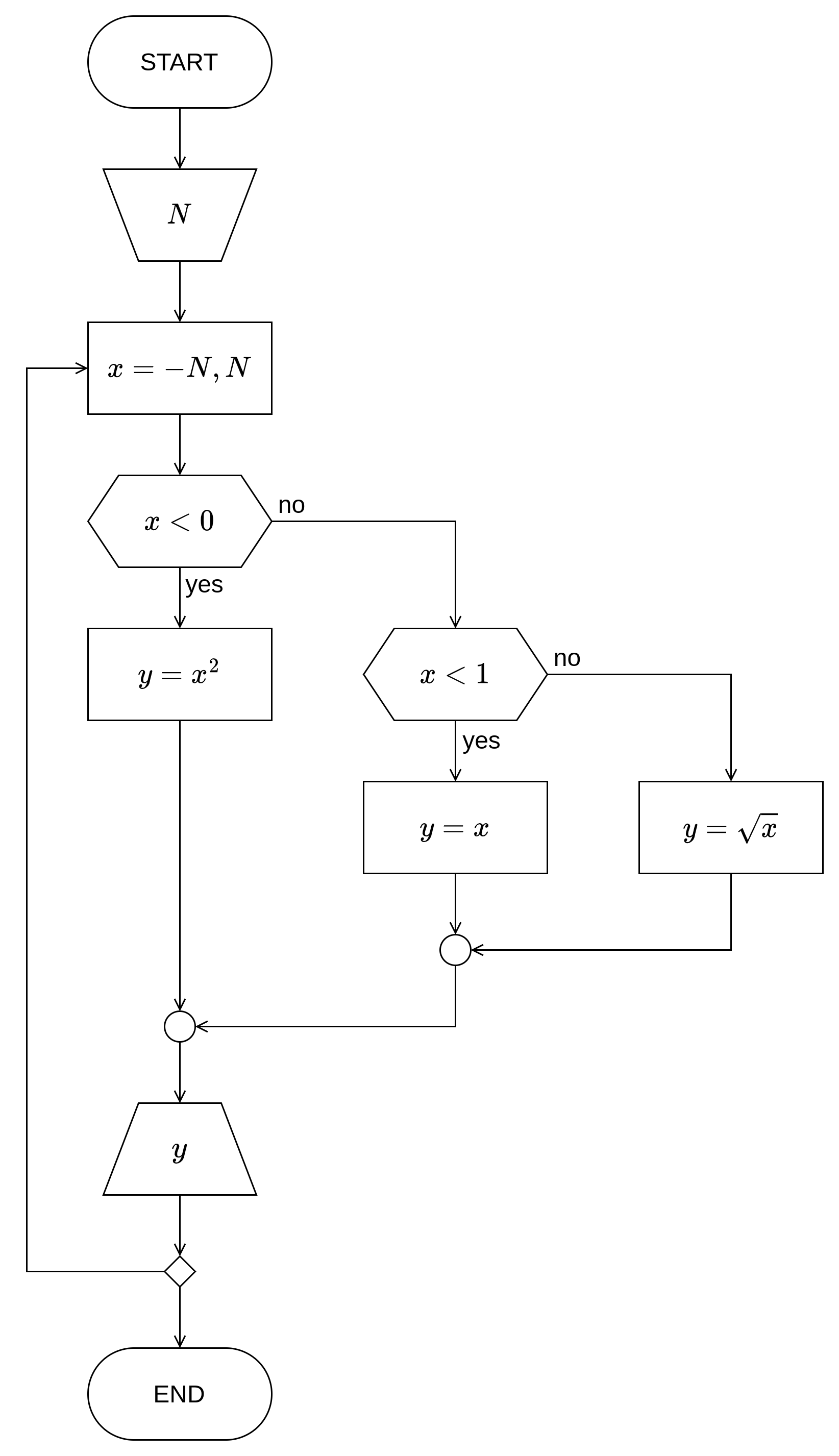
Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм којим се у бројачкој петљи за целобројне вредности аргумента \(x\) из интервала од \(-N\) до \(N\) израчунава вредност \(y\) као:

\[ y = \begin{cases} x^2, & x < 0 \\ x, & 0 \leq x < 1 \\ \sqrt{x}, & x \geq 1 \end{cases} \]

Целобројни параметар \(N\) уноси корисник. Уколико се при извршавању програма за \(N\) унесе вредност \(5\), шта ће програм приказати на излазу?

Дијаграм тока алгоритма

Изворни код програма

if-elseТернарни оператор

#include <stdio.h>
#include <math.h>

main() {
    int n, x;
    double y;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (x = -n; x <= n; x++) {
        if (x < 0) {
            y = pow(x, 2);
        } else if (x < 1) {
            y = x;
        } else {
            y = sqrt(x);
        }

        printf("x = %d; y = %g\n", x, y);
    }
}

#include <stdio.h>
#include <math.h>

main() {
    int n, x;
    double y;

    printf("Unesite ceo broj N: ");
    scanf("%d", &n);

    for (x = -n; x <= n; x++) {
        y = x < 0 ? pow(x, 2) : x < 1 ? x : sqrt(x);

        printf("x = %d; y = %g\n", x, y);
    }
}

Задатак 8.

Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм који решава једначину \(x^2 + 3\sqrt{x} + 2 = 0\) применом следећег итеративног поступка:

\[ x_0 = 0; \\ x_{i+1}=\frac{3x_i^4+4x_i^2-4}{4x_i^3+8x_i-9}, i = 0, 1, 2, … \]

Израчунавање прекинути када је \(|x_{i+1}-x_i| \leq e\), где је \(e\) реални број који представља задату тачност. Уколико се при извршавању програма за \(e\) унесе вредност \(0{,}00001\), шта ће програм приказати на излазу?

Дијаграм тока алгоритма

Изворни код програма

#include <stdio.h>
#include <math.h>

main() {
    double x0, x = 0, e;

    printf("Unesite e: ");
    scanf("%lf", &e);

    do {
        x0 = x;
        x = (3*pow(x0, 4) + 4*pow(x0, 2) - 4) / (4*pow(x0, 3) + 8*x0 - 9);
    } while (fabs(x - x0) > e);

    printf("x = %lf\n", x);
}

Задатак 9.

Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм који одређује и приказује вредност функције \(exp(x)\), за аргумент \(x\) који је реалан број, применом развоја у ред:

\[ exp(x) = \sum_{n=0}^{\infty} \frac{x^n}{n!} \]

Израчунавање прекинути када релативна вредност прираштаја суме постане мања од задате тачности \(e\) која је такође реалан број. Уколико се при извршавању програма за \(e\) унесе вредност \(0{,}00001\), а за \(x\) унесе \(3\), шта ће програм приказати на излазу?

Дијаграм тока алгоритма

Изворни код програма

#include <stdio.h>
#include <math.h>

main() {
    double e, x;
    long double exp = 0, prev, a = 1, b = 1;
    int n = 0;

    printf("Unesite vrednost е: ");
    scanf("%lf", &e);

    printf("Unesite vrednost x: ");
    scanf("%lf", &x);

    do {
        n++;
        prev = exp;

        exp += a / b;
        a *= x;
        b *= n;
    } while (fabsl(prev - exp) >= e);

    printf("%Lf\n", exp);
}

Задатак 10.

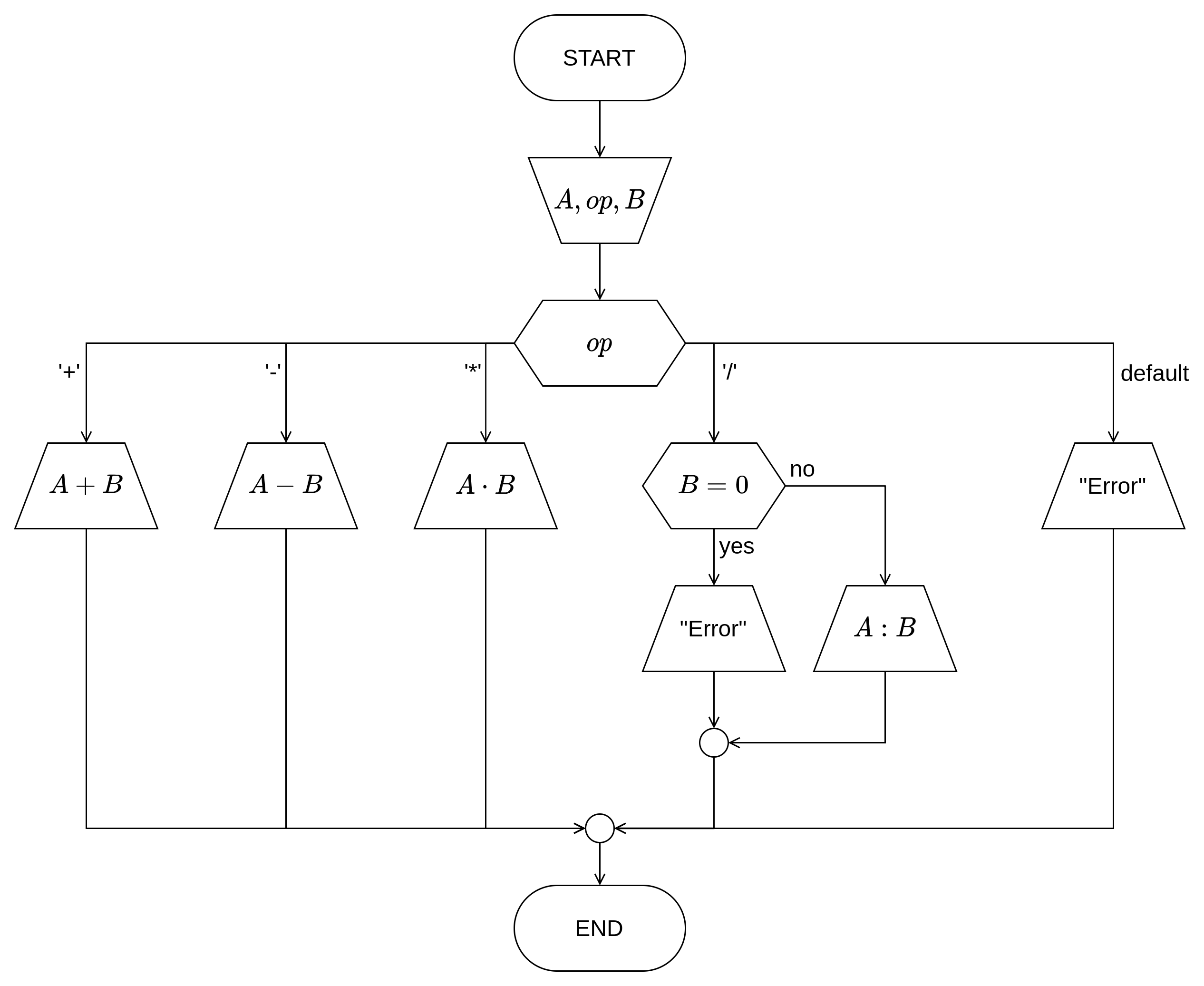
Нацртати структурни дијаграм тока алгоритма и на програмском језику C написати структурни програм за израчунавање једноставних израза типа \(A\ op\ B\), где су \(A\) и \(B\) реални бројеви, а операција \(op\) се задаје карактером +, -, * или /. Приказати добијени резулатат.

Напомена

Декларацију променљивих и уноса израза реализовати на следећи начин:

    float A, B;
    char op;
    scanf("%f%c%f", &A, &op, &B);

Уколико се при извршавању програма унесе 8/3, шта ће програм приказати на излазу?

Дијаграм тока алгоритма

Изворни код програма

switch-caseif-else"

#include <stdio.h>

main() {
    float A, B;
    char op;

    scanf("%f%c%f", &A, &op, &B);

    switch (op) {
        case '+':
            printf("%g\n", A + B);
            break;
        case '-':
            printf("%g\n", A - B);
            break;
        case '*':
            printf("%g\n", A * B);
            break;
        case '/':
            if (B == 0) {
                printf("Greska, deljenje nulom nije definisano!\n");
            } else {
                printf("%g\n", A / B);
            }
            break;
        default:
            printf("Greska, nepoznata operacija!\n");
            break;
    }
}

#include <stdio.h>

main() {
    float A, B;
    char op;

    scanf("%f%c%f", &A, &op, &B);

    if (op == '+')
        printf("%g\n", A + B);
    else if (op == '-')
        printf("%g\n", A - B);
    else if (op == '*')
        printf("%g\n", A * B);
    else if (op == '/')
        if (B == 0)
            printf("Greska, deljenje nulom nije definisano!\n");
        else
            printf("%g\n", A / B);
    else
        printf("Greska, nepoznata operacija!\n");

}

Mодификација задатка

Шта уколико се тражи да програм рачуна вредност израза типа \(A\ op1\ B\ op2\ C\)?

#include <stdio.h>
#include <stdlib.h>

main()
{
    char op1, op2;
    double a, b, c;

    scanf("%lf %c %lf %c %lf", &a, &op1, &b, &op2, &c);

    if (op1 == '/') {
        if (b == 0) {
            printf("Deljenje nulom nije definisano!");
            exit(1);
        }

        b = a / b;
    } else if (op1 == '*') {
        b = a * b;
    }

    if (op2 == '/') {
        if (c == 0) {
            printf("Deljenje nulom nije definisano!");
            exit(1);
        }

        b = b / c;
    } else if (op2 == '*') {
        b = b * c;
    }

    if (op1 == '+') {
        b = a + b;
    } else if (op1 == '-') {
        b = a - b;
    }

    if (op2 == '+') {
        b = b + c;
    } else if (op2 == '-') {
        b = b - c;
    }

    printf("%g\n", b);
}